Supporting Mixtral in gpt-fast through torch.compile [short]

Long-form version of this tweet thread: https://twitter.com/cHHillee/status/1762269069351461196

About 2 months after the work was actually done, we finally merged mixtral support into gpt-fast! Check the code out here: https://github.com/pytorch-labs/gpt-fast/tree/main/mixtral-moe

Featuring:

• (!) no custom kernels

• int8 and tensor-parallelism support

• still very simple (<150 LOC to support)

• faster decoding than any (non-Groq) API endpoint, at up to 220 tok/s/user with A100s.

Bonus: Running on a H100 node, we can get closer to 300 tok/s/user!

Faster decoding than any non-Groq endpoint! (at Feb 26th 2024)

We thought it might be interesting to talk a bit about why this is a bit tricky and how we solved it.

Mixture of Experts (MoE) vs. Dense Transformers

Unlike Llama, Mixtral is a sparse architecture. The main idea here is that instead of a single dense layer with eight thousand parameters, we split it into 8 “experts”, where each expert is a dense layer with only one thousand parameters. Then, depending on some dynamic information, we only “activate” 2 out of the 8 experts for each layer.

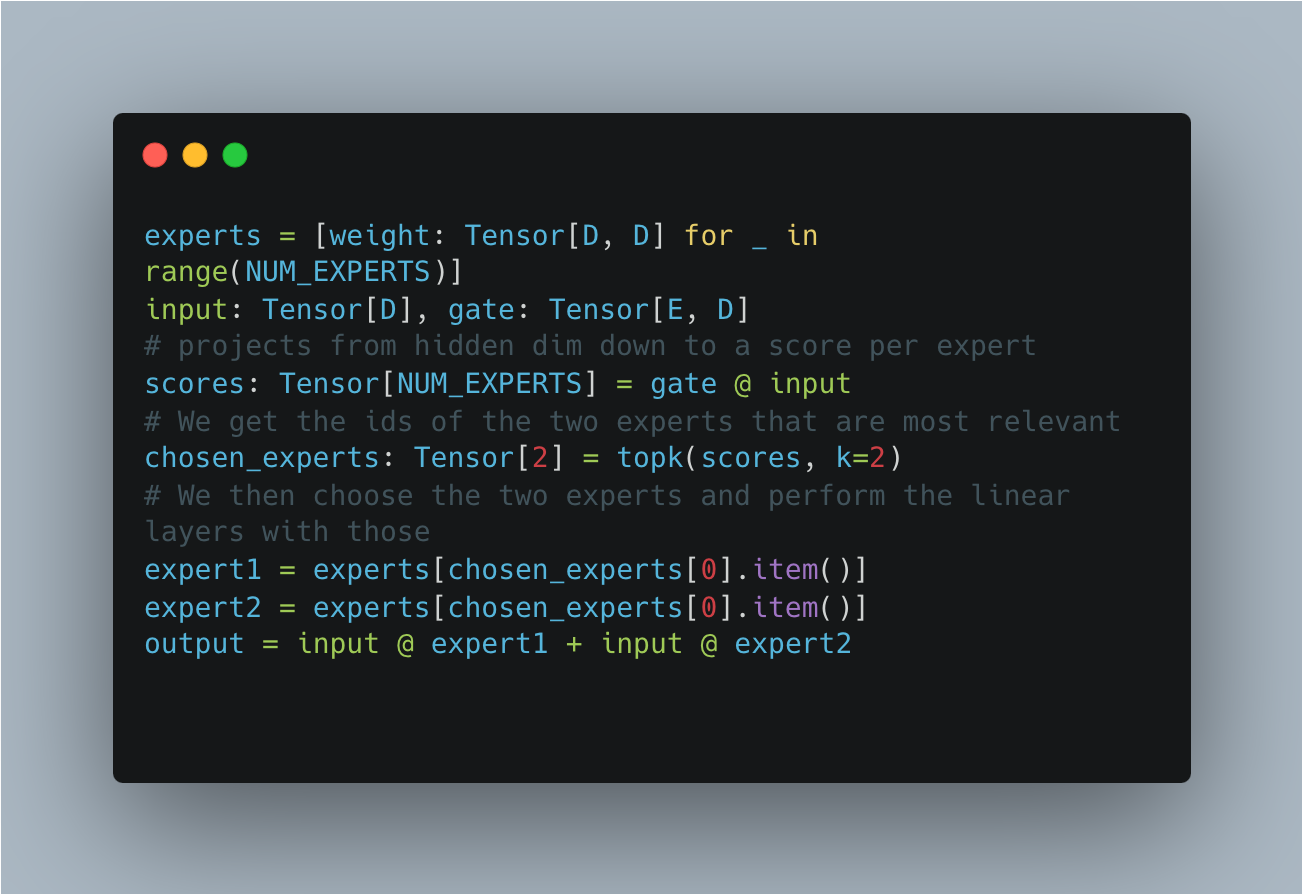
Morally, this is easy to implement for each token.

Crucially, note that out of the 8 experts that constitute our weights, 6 of them do nothing for any token, making mixture of experts a “sparse” model.

For those who have experience with performant PyTorch, you may be wincing. Using a tensor to index into a python list is a cardinal performance sin (it induces a cuda sync, where the CPU waits for the GPU).

This is the difficulty with running Mixtral efficiently.

The runtime advantage of MoE comes from dynamic sparsity. But if this dynamism isn't handled efficiently, you might end up slower than if you had no sparsity to begin with.

Moving the Dynamism “onto” the GPU

Luckily, there’s another option that works well for BS=1 decoding. Instead of doing the indexing in Python, let’s do the indexing on the GPU. In other words, let’s do the indexing using a “gather” operation.

A gather operation occurs when you decide to load from a tensor using another tensor. In PyTorch, this is often done using what’s called “advanced indexing”. For example:

primes = torch.tensor([2, 3, 5, 7, 11])
b = torch.tensor([1, 3, 0])
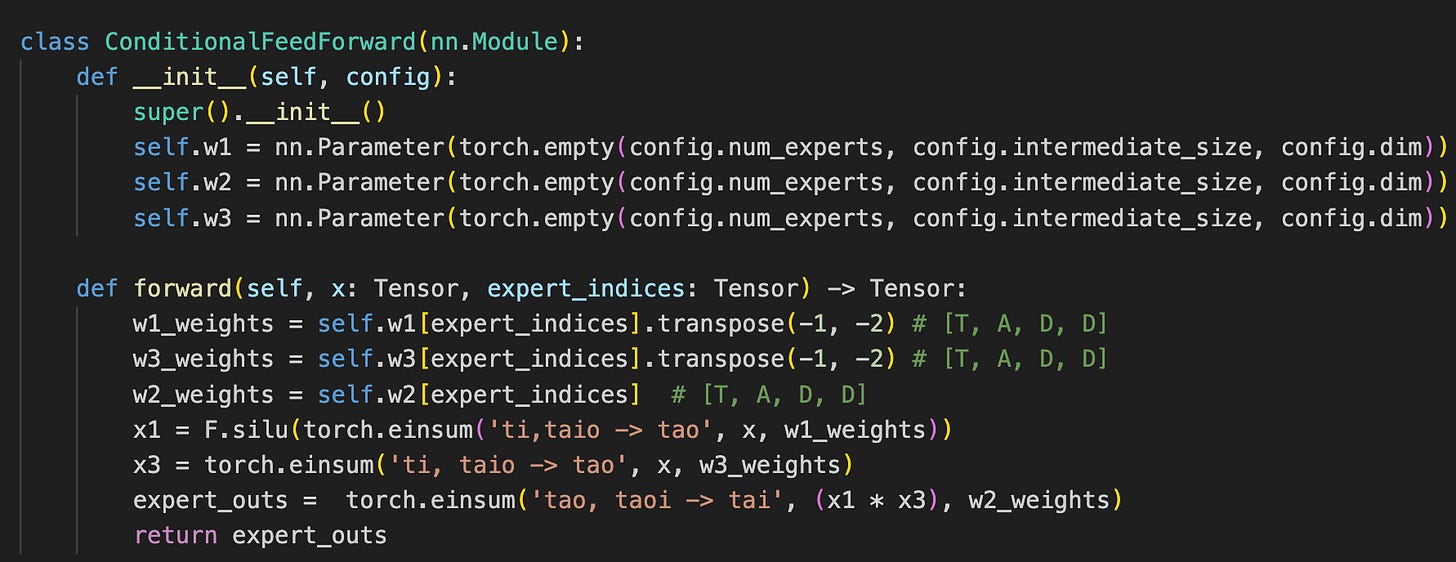
primes[b] # tensor([3, 7, 2])

So, putting it all together, our full MoE layer looks morally like this.

The full FFN layer looks a bit more different since we need to handle multiple tokens as well as multiple FFNs in a row, but it’s morally the same idea. Note: this is the primary implementation difference between regular dense transformers and Mixture of Experts!

This implementation approach has two main advantages - it doesn't require any synchronizations and only uses weights required for computation. However, if we run this normally, we have another issue. Both the gather operation and the actual linear layer itself requires us to touch DRAM with all of the weights we’re using. This is a factor of 3 slowdown.

Luckily, PyTorch now has a compiler.

Torch.compile to the rescue!

Torch.compile can fuse the gather + gemv into one kernel, allowing us to obtain our theoretical speedups.

If you’re curious to look at the Triton kernel generated by torch.compile, you can see it here.

Concretely, this is the indirect access/gather. Bolding added to emphasize the main operations involved.

tmp0 = tl.load(in_ptr0 + (r2 + (4096*x1)), None, eviction_policy='evict_last').to(tl.float32)
tmp1 = tmp0.to(tl.float32)
tmp3 = tmp2 + 8
tmp4 = tmp2 < 0
tmp5 = tl.where(tmp4, tmp3, tmp2)
tmp6 = tl.load(in_ptr2 + (r2 + (4096*(x0 % 14336)) + (58720256*tmp5)), None, eviction_policy='evict_first')
tmp7 = tmp6.to(tl.float32)
tmp8 = tl.load(in_ptr3 + ((14336*tmp5) + (x0 % 14336)), None, eviction_policy='evict_first').to(tl.float32)

Let’s also validate the performance with a benchmark.

def cuda_indexing(W, score_idxs, x):
    return W[score_idxs] @ x

def python_indexing(W, score_idxs, x):
    return W[score_idxs[0]] @ x, W[score_idxs[1]] @ x

W = torch.randn(E, D, D)
x = torch.randn(D)
score_idxs = torch.tensor([3, 5])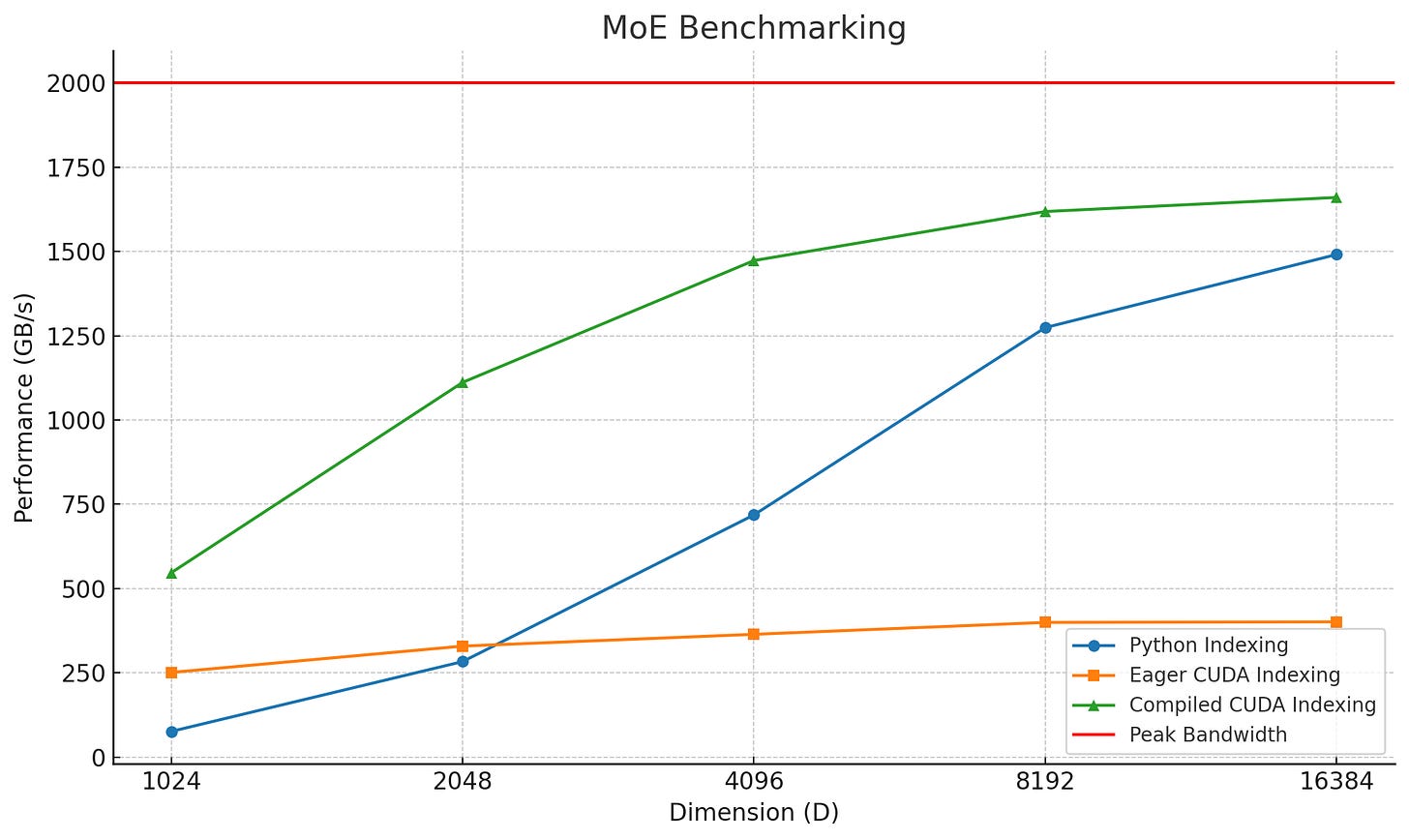

Note that at (smaller) dimension sizes, cuda indexing + torch.compile substantially outperforms python indexing. At larger dimensions the overhead starts to matter less and less, but torch.compile still stays quite performant.

End to End Benchmarks

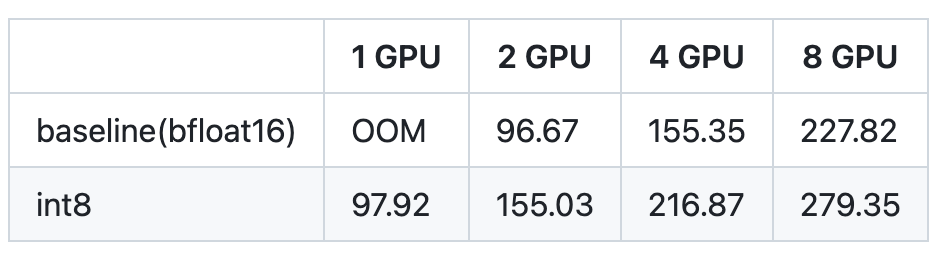
Combining this altogether into an E2E benchmark, we see that for int8 on a single A100, we run at 98 tok/s. Note that if this were a dense model, we would effectively be running at 4.55 TB/s of bandwidth, which is higher than the theoretical limit!

Of course, combining it with tensor-parallelism, we can get up to 280 tok/s! Note that this is all for BS=1, so this is “tok/s/user for only output tokens”.

Considering that this is faster tokens/s than any (non-Groq) API provider, we think this is pretty impressive.

Moreover, since we codegen into Triton, we should also be able to run on AMD as well. We’ll update this post when we get those results.

Of course, we will also mention the typical gpt-fast caveats. This is optimized for latency and not throughput. In this particular case, the strategy we use for BS=1 codegen scales very poorly to larger batch sizes.

Nevertheless, we think that this continues to demonstrate the gpt-fast ethos. Simple, native PyTorch, and very fast!