Strangely, Matrix Multiplications on GPUs Run Faster When Given "Predictable" Data! [short]
Great minds discuss flops per watt.
It’s 2022. I check out this cool new project, CUTLASS, with very fast matmuls. I take a large matmul, 8192 x 8192 x 8192, and benchmark it in PyTorch, which calls CuBLAS.
python mm_bench.py
> CuBLAS: 258 TeraflopsNot bad, 83% flop utilization. Now let’s check out Cutlass’s performance using their profiler.
./cutlass_profiler --operation=Gemm --m=8192 --n=8192 --k=8192
> CUTLASS: 288 Teraflops!!! 10% higher perf? That’s incredible. CuBLAS is highly optimized for large compute-bound matmuls, and somehow CUTLASS + autotuning is outperforming it by 10%? We gotta start using these matmuls yesterday.
The next step is to bind the CUTLASS kernels into Python and compare against CuBLAS using my previous script.
python cutlass_mm_bench.py
> CuBLAS: 258 Teraflops
> CUTLASS: 257 TeraflopsSomehow, in the light of Python, all of CUTLASS’s performance gains disappear. This in of itself is not shocking - it’s notoriously difficult to ensure consistent benchmarking across setups.
I tediously ablate the two benchmark scripts, until finally, I find that CUTLASS’s profiler, by default, actually initializes the values in a fairly strange way - it only initializes the inputs with integers. Confused about whether this matters, I try:
zero_inputs = torch.zeros(N, N)
randn_inputs = torch.randn(N, N)
benchmark(zero_inputs) # 295 Teraflops
benchmark(randn_inputs) # 257 TeraflopsWhat? How could the values of the matrix affect the runtime of the model? I know Nvidia has some weird data compression thing on A100s, but I wouldn’t have expected that to be on in matmuls. Let’s try some other data distributions, like an uniform distribution [0,1].
This was … confusing, to say the least. Somehow, the actual content of the tensors being multiplied is leading to different matmul performance.
There certainly are cases where the runtime depends on the content of the tensor — indirect indexing (e.g. A[b]), or things like sparsity.
But matrix multiplications have nothing like that at all! No matter what the contents of the matrix contain, the matrix multiplication kernel will 1. perform the same number of computations, 2. perform the same computations in the same order, 3. access the same memory addresses, and 4. access the same memory addresses in the same order.
Nowhere did my mental model of matrix multiplications and GPU hardware allow for the values in the matrix to influence matmul performance. And yet, here we are.
As it turns out, the culprit is ……. dynamic/switching power in semiconductors!
Power Usage in Semiconductors
An Nvidia A100 GPU has a power limit of 400W1. However, as the phrase “power limit” may hint, the GPU doesn’t always use all 400W. For example, when the GPU is fully idle, nvidia-smi tells me that it’s only pulling 88W of power.
But when the GPU is running under load, that power usage will spike considerably, typically to around the power limit.
In order to stay under the power limit, a piece on the chip called the Voltage Regulator Module reduces the voltage supplied to the GPU, — throttling the clock frequency and reducing its performance.
In other words, if our GPU ends up using enough power to hit the power limit, our performance will become capped.
Most of us take it for granted that “GPU does something, power consumption goes up”. But there are actually two distinct mechanisms through which power gets consumed.
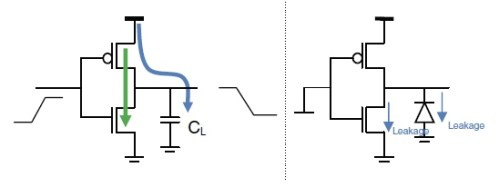
The first one is static/leakage power. You can think of this as the power that inevitably gets lost by just flowing power through your circuits. The amount of static power used is proportional the amount of silicon that is powered. As GPUs don’t do much power gating, this is essentially the amount of power used at idle (88W in the above photo).
However, the second one, dynamic (or switching) power, is the culprit. Specifically, a small amount of power is consumed whenever a transistor switches states. If the transistor never needs to switch states, it doesn’t consume any extra power. On the other hand, if it’s rapidly flipping, then it consumes a ton of dynamic/switching power. Multiply that by the billions of transistors in your GPU, and you get the overall increase in power consumption.
In other words, the reason why matrix multiplications are faster when passed zeros is that this reduces the “flipping” of enough transistors in the chip to stay under the power limit!
So, this (mostly) explains what we saw previously2. All zeros are probably the fastest since every single bit of each computation is a zero and the accumulator remains at zero. All ones is probably still quite fast since every single tensor-core instruction results in exactly the same values. The uniform distribution probably is a little bit faster than the normal distribution since the accumulator never needs to flip-flop between positive and negative. The normal distribution probably has the worst performance since it leads to pretty high randomness among all transistors involved in the computation(?).
Here’s the results on a number of fun distributions I tried:
Randn: Normally distributed
Checkerboard: Normal distribution, but we have zeros in a checkerboard shape.
Rand: Uniform distribution
Sparse: Normal distribution, but a (random) 75% of the elements are masked.
Ternary: Every value is 1, -1, or 0.
One Bit: Only one bit set in every single value (the 4th bit)
All Pies: Every single value is the mathematical constant PI.
Twos: Every value in the matrices are 2
Zeros: Every value in the matrices are 0
Who says unstructured sparsity isn’t efficient with tensor-cores? :)
How power limit and clock speed affects this
Here’s another piece of evidence that dynamic/switching power is responsible.
Roughly, the power we’re using is proportional to the clock speed multiplied by amount of transistor flips we’re doing.
power ~= clock speed * “transistor flips per clock”.
We run into throttling when the power we use surpasses the power limit we’ve set. Thus:
If we reduce our power limit we exacerbate this effect.
If we reduce the clock speed we reduce this effect.
Let’s show that in action! To do so, I’ll compare the relative performance of a very predictable input (zeros) vs a very unpredictable input (randn).
As expected, we see that as the power limit decreases from 330W down to 100W (the minimum), the relevant performance improvement from using predictable inputs increases. Interestingly, at the lowest power limit (100W), the trend reverses. I’m guessing that the GPU is so power constrained that even using all zeros still results in too much power usage. [Uma Kelkar in the comments suggests that this is because throttling the power limit also just directly throttles the clock speeds]. Remember that the switching power is coming from every transistor in the GPU, not just the ones holding data! So that includes the transistors for say, keeping track of the current program counter, keeping track of how many loop iterations you need to perform, the ones signaling other transistors to perform operations, pretty much everything that a GPU can possibly be doing.
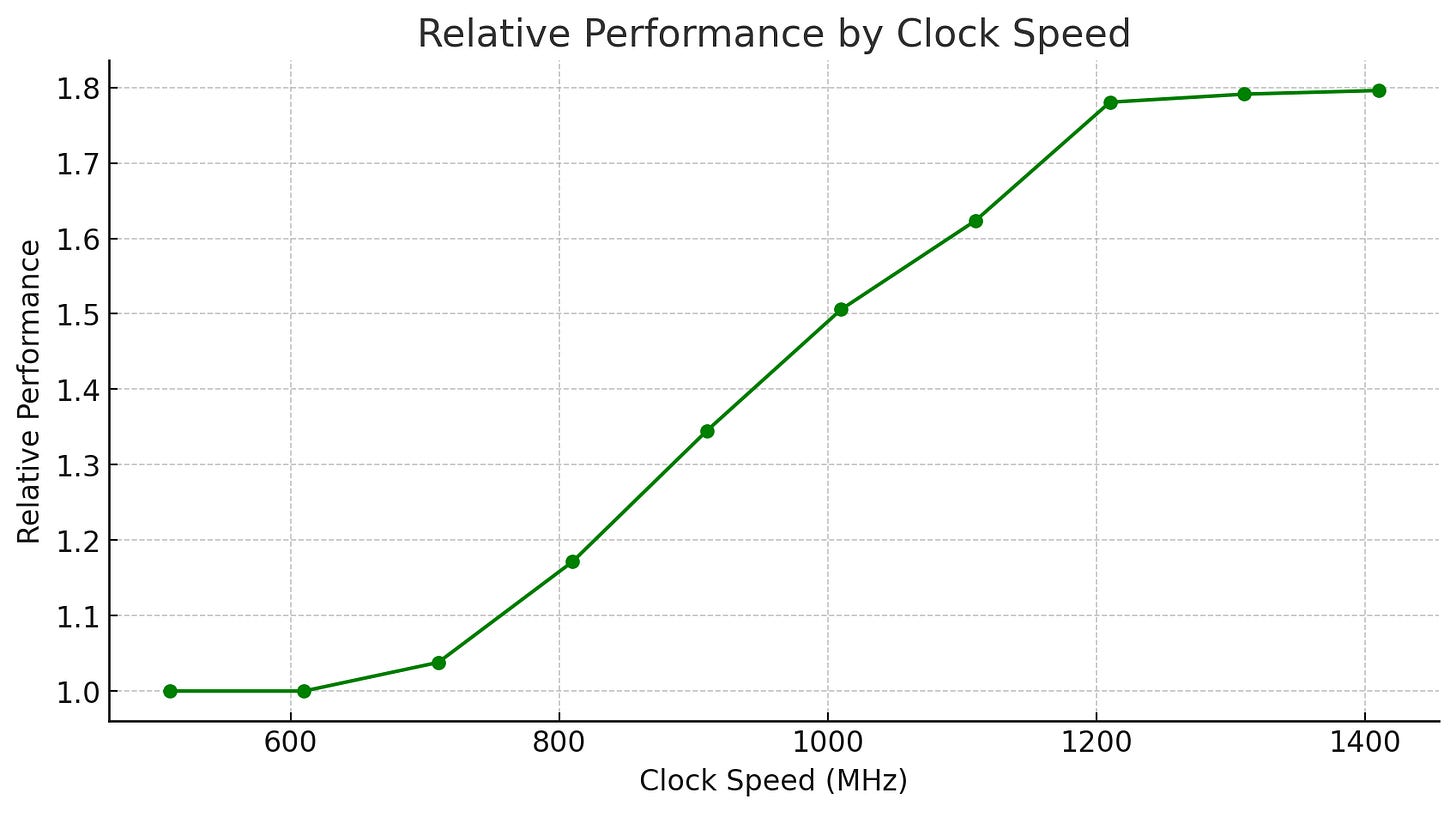
Now, to test the effect of GPU clocks on using predictable vs. unpredictable inputs, I’ll use a a power limit of 200 and vary the GPU clock limit.
We see that at the top range of the clock frequency, there is nearly no change in the ratio, as presumably even with predictable inputs, we’re still getting throttled. Then, as we decrease the clock speed, the relative gap shrinks as predictable inputs are affected by the clock speed limit, but not unpredictable inputs. Finally, at the very left of the chart, both using predictable and unpredictable inputs have identical performance, as both become completely limited by our manual clock speed limit and don’t do any power throttling.
Another interesting thing we can test is, for a given input and power limit, what is the maximum clock speed the GPU can sustain for a matmul?
Marketing vs “Real” Performance
This observation that GPUs are unable to sustain their peak clock speed due to power throttling is one of the primary factors that separates “real” matmul performance from Nvidia’s marketed specs.
The figure that Nvidia provides for marketing is:
For example, on an H100, there are 528 tensor cores per GPU (4 per SM), the max clock speed for these is 1.830 Ghz, and the FLOP per tensor-core instruction is 1024. Thus, we have 1.830e9 * 528 * 1024 = 989 TFLOPS, exactly Nvidia’s listed number.
However, you can only achieve this number by sustaining 1.83 Ghz clocks, and as we’ve seen above, the GPU just doesn’t have enough power to do that!
Do note that in both of these cases, the GPUs have a higher power limit than I can test (400W on A100 and 700W on H100 respectively), so it’s able to sustain a higher clock speed than what’s charted here. But we can see that, especially on the H100, the max sustainable clock speed is much lower than the theoretical one! In other words, matmuls on the H100 are primarily not compute or bandwidth limited, they are power limited.
As many have noted, power is increasingly a crucial constraint. So, although the H100 theoretically had 3x more FLOPS than the A100, its “real” performance has usually been closer to 2x due to the power throttling we’ve been discussing, and its “flops per watt” is even less than that.
Update (6/25): Nvidia recently released their MLPerf submission which largely confirms the hypothesis in this blog post. Thanks Sophia Wisdom for the pointer!
This leads to high Tensor Core utilization and can result in scenarios where Tensor Core throughput is constrained by the power available to the GPU.
In the submission with 512 H100 GPUs, we improved end-to-end performance by redirecting power from the L2 cache memory on each H100 GPU to the streaming multiprocessor (SM), which houses, among other units, NVIDIA Hopper fourth-generation Tensor Cores.
Conclusion
All of this should make you exceedingly curious to see the actual performance improvement on the B100, which has a 1.75x theoretical increase in FLOPS with the same power usage as the H100. I have a Manifold market about guessing the max FLOPS utilization on a B100.
I’ll leave you with a slightly modified version of this tweet from roon.
Thanks to Sophia Wisdom, Vijay Thakkar, Philippe Tillet, Dylan Patel, and Natalia Gimelshein who have helped me understand this phenomenon.
Also, be aware that you need to set the `scale` parameter on the CUTLASS profiler if you wanna compare its FLOPS numbers to other benchmarks!
The A100 GPU I’m testing this on happens to have a power limit of 330W.
It’s hard for me to say for sure, since I can’t count how many times each individual transistor flips :)










Benchmark performance by input type chart for H100, H200, MI300X pls. Make it something I gotta pay for lol. It would be cool to see FLOPS/Watt across all those HW too, cause rn all we see is some random MFU across a whole model which isnt apples to apple or theoretical peaks.
Very nice article, Horace.
It’s something many of us have long suspected, but this is the first time I am seeing actual experimental results showing that peak flops are really just pie in the sky — even if memory bandwidth was infinite.